书接上文。上一篇文章中使用麦克斯韦方程组推导了磁环电感和带有气隙的C字形磁环电感的电感量表达式。虽然说麦克斯韦方程组通杀一切电磁现象，但是每次推导都要列一大堆公式，我们仅仅只是设计一个相对低频的功率磁性器件，没有必要这么“大动干戈”。下面介绍一种更简单的，将磁路等效为电路分析的方法。

最简单的电路

首先想让我们思考一下，要构建一个最简单的电路，需要有哪些部分组成。
第一个想到的东西当然是源。不管是电压源还是电流源，独立源还是受控源，整个电路运转的动力都由这个源来提供。
第二个就是负载。既然源提供了动力，那么这些能量就要有消耗的地方，不然这个源放那儿也没有什么意义了。
第三个就是存在完整回路，将源和负载联系起来。

电路中的“流通量”，即为电流$I$：

类比

磁路和电路类似，在磁芯中也存在某种“流通量”——磁通$\phi$，回顾一下上面两种磁芯中$\phi$的表达式：

似乎和上面电流的表达式有一点形似：

把电阻改写成带电导率$\sigma$的表达式：

这下看起来形式就一模一样了。

磁动势 $\mathfrak {F}$

通过上面的讲解，可以把$Ni$和$V$类比成一样的东西，我们称为磁动势，用字母${\mathfrak {F}}$表示：

磁阻 ${\mathfrak {R}}$

自然，磁动势下面除的那个东西就可以称作磁阻，用字母${\mathfrak {R}}$表示：

磁压降

一个磁阻${\mathfrak {R}}$通过大小为$\phi$时两端产生的压降称为磁压降$U_m$：

磁链

磁链就可以表示成：

电感

电感量就可以表示成：

磁路中的KVL和KCL

有了上面的假设，我们可以推导一下磁路中的KVL和KCL，看看是否真的和电路的形式一样。

1. KCL
   根据磁通连续性定理 $\oint_S\vec{B}\cdot\mathrm{d}\vec{S}=0$，通过每个截面的磁通$\phi$必须相同，净流入磁通等于净流出磁通，自然是满足KCL的描述的。

2. KVL
   根据安培环路定律有：

   $$\oint_{l}\vec{H}\cdot\mathrm{d}\vec{l}=\sum_{i=1}^nI_i=NI$$

   同时磁动势$\mathfrak {F}=NI$。
   为了简化左边的环路积分，我们假设：

   • 在磁芯的任一横截面上，磁场强度$H$是均匀的。
   • 磁场方向始终与积分路径的切线方向一致。

   那就可以把积分路径分为$m$段：

   $$\oint_{l}\vec{H}\cdot\mathrm{d}\vec{l}=H_1l_1+H_2l_2+...+H_ml_m=\sum_{i=1}^mH_il_i$$

   由${{H} ={\frac {{B} }{\mu}}}$和$B=\phi A$得到：

   $$H_k=\frac{B_k}{\mu_k}=\frac{\phi}{\mu_k A_k}$$

   则：

   $$\sum_{i=1}^mH_il_i=\sum_{i=1}^m\frac{\phi}{\mu_k A_k}l_i=\phi\sum_{i=1}^m\frac{l_i}{\mu_k A_k}=\phi\sum_{i=1}^m{\mathfrak {R}}_{k}$$

   那就是：

   $$\oint_{l}\vec{H}\cdot\mathrm{d}\vec{l}=NI=\sum_{i=1}^mH_il_i=\phi\sum_{i=1}^m{\mathfrak {R}}_{k}=\mathfrak {F}$$

   最后就得到这些东西：

   1. 磁路的全欧姆定律：
      $${\displaystyle {\mathfrak {F}}=\Phi {\mathfrak {R}}_总} <=> {\mathcal {E}}=IR_总$$
   2. 左边磁压升等于右边磁压降：
      $$NI=\Phi {\mathfrak {R}}_总$$
      或者
      $$\sum NI=\sum Hl$$

   沿任何闭合磁路，各段磁路上的磁压降$Hl$的代数和，等于围绕此回路的所有磁动势$Ni$的代数和。

带有气隙的C字形磁环电感的磁路模型

有了上面的电路等效，上一篇文章最后的带有气隙的C字形磁环电感的磁路模型就可以画成这样：
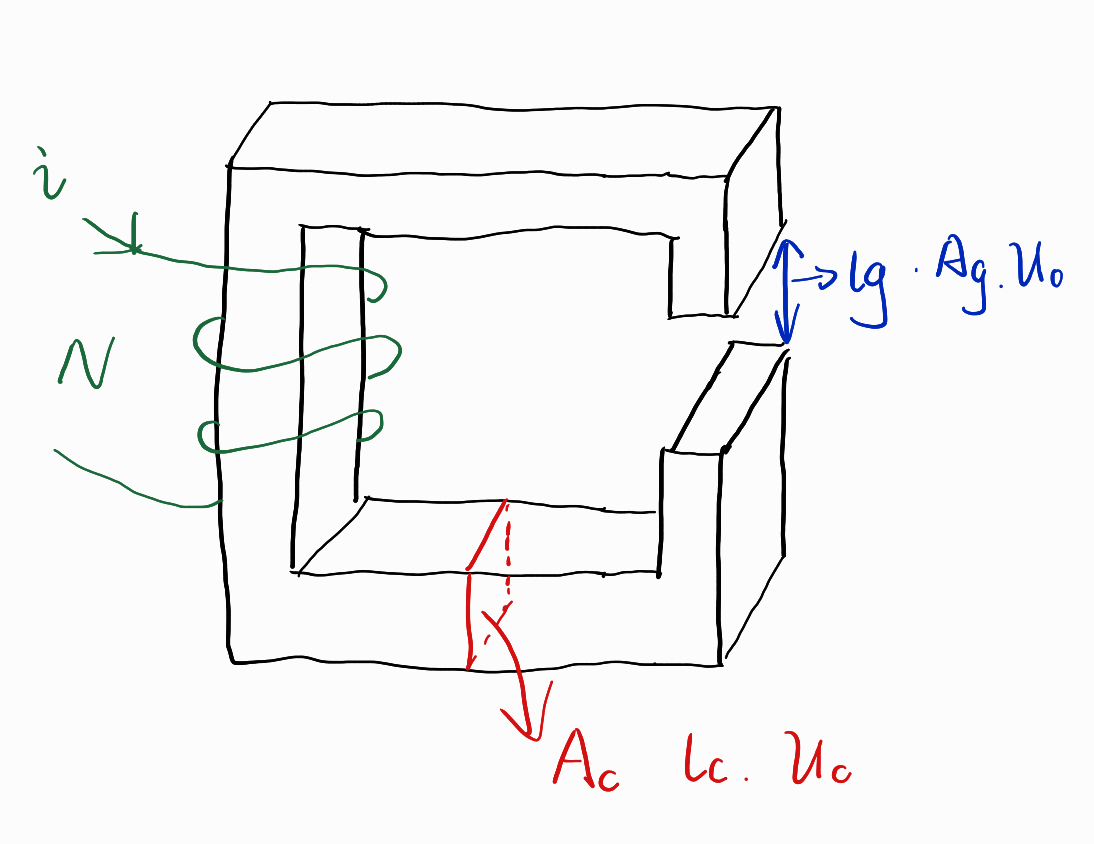
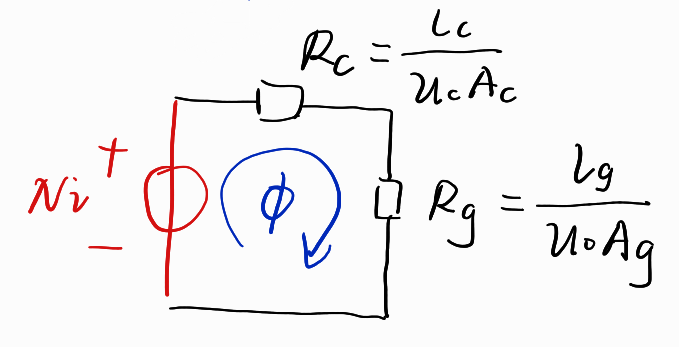
因为$\mu_c$>>$\mu_0$，所以${\mathfrak {R}}_c$<${\mathfrak {R}}_g$，又只有一个回路，所以${\mathfrak {R}}_c$上的磁压降小于${\mathfrak {R}}_g$上的磁压降。如果像电路那样计算电阻上面的功率，那磁阻上面的功率就是${\mathfrak {R}}_c$上的"磁功率"小于${\mathfrak {R}}_g$上的“磁功率”，这从另一个方面印证了磁芯的大部分能量都存储在气隙里面。