zxcli的博客
磁性器件学习笔记（一）
2025-10-25
硬件学习笔记
00
磁性器件电感计算

目录

基础知识
相关物理量
麦克斯韦方程组
电感方程
伏秒积(电压型方程)
电流型方程
磁环电感
电感量推导
初步设计磁环电感
带有气隙的C字形磁环电感

之前手写了一堆磁性器件学习笔记，这里规范下公式啥的，整理一下写几篇博客。资料来源有MIT的2023春季电力电子公开课、赵科修老师的《开关电源中的磁性器件》、Sanjaya Maniktala的《精通开关电源设计》第二版以及B站的一些视频。

基础知识

相关物理量

  1. 磁感应强度(磁通密度) BB：
    衡量磁场强弱的物理量。

  2. 磁通量 ϕB{\displaystyle \phi _{B}}：
    是通过某给定曲面S的磁通密度的大小的度量。

    ϕB=∬SB⋅dS{\displaystyle \phi _{B}=\iint \limits _{S}\mathbf {B} \cdot d\mathbf {S} }

    均匀磁场垂直射入平面SS时，就是

    ϕB=B⋅S(1.1.1)\phi _{B}=B \cdot S \tag{1.1.1}

  3. 磁导率 μ\mu
    表征物质导磁能力的物理量。
    μ\mu越大，相同电流和匝数的线圈在该物质内产生的磁感应强度越大。
    为了便于记忆和计算，把其他材料磁导率μ\mu与真空磁导率μ0\mu_0的比值称为相对磁导率μr=μμ0\mu_r = {\frac {\mu}{\mu_0}}。

  4. 磁场强度 HH
    在物质内部：

    H=Bμ(1.1.2){{H} ={\frac {{B} }{\mu}}} \tag{1.1.2}

  5. 磁链 λ\lambda (或者 ψ\psi)
    一匝线圈产生(或通过)的磁通量是ϕ{\displaystyle \phi}，与NN匝紧密缠绕且无漏磁线圈相交链的总磁通称为磁链：

    λ＝Nϕ(1.1.3)λ＝N\phi \tag{1.1.3}

  6. 自感(或者电感) LL
    磁链λ\lambda由通入的电流ii产生，如果物质的磁导率μ\mu为常数时， 磁链λ\lambda和电流ii呈线性关系：

    λ=Li(1.1.4)\lambda=Li \tag{1.1.4}

麦克斯韦方程组

下面的推导不需要用到完整形式的麦克斯韦方程组，基本上只用考虑最简单的情况即可：磁芯横截面形状规则，磁芯内部是匀强磁场且与横截面垂直。

  1. 安培环路定律：
    在稳恒磁场中，磁感应强度B沿任何闭合路径的线积分，等于这闭合路径所包围的各个电流的代数和乘以磁导率。

    ∮lB⋅dl=μ0∑i=1nIi\oint_{_l}B\cdot dl=\mu_0\sum_{i=1}^nI_i

    或者

    ∮lH⃗⋅dl⃗=∫sJ⃗⋅dS⃗=∑i=1nIi（只考虑静磁场）(1.2.1)\oint_{l}\vec{H}\cdot\mathrm{d}\vec{l}=\int_{s}\vec{J}\cdot\mathrm{d}\vec{S}=\sum_{i=1}^nI_i \tag{1.2.1}（只考虑静磁场）

  2. 法拉第电磁感应定律
    任何封闭电路中感应电动势大小，等于穿过这一电路磁通量的变化率。

    ∮lE⃗⋅dl⃗=−∫s∂B⃗∂t⋅dSˉ\oint_{l}\vec{E}\cdot\mathrm{d}\vec{l}=-\int_{s}\frac{\partial\vec{B}}{\partial t}\cdot\mathrm{d}\bar{S}

    只考虑最简单的情况时：

    E=−NdΦBdt(1.2.2){\displaystyle {\mathcal {E}}=-{N\frac {d\Phi _{B}}{dt}}} \tag{1.2.2}

    E\mathcal {E}是电动势，NN是线圈匝数。

  3. 磁通连续性定理

    ∮SB⃗⋅dS⃗=0\oint_S\vec{B}\cdot\mathrm{d}\vec{S}=0

电感方程

由法拉第电磁感应定律-式(1.2.2)、磁链定义-式(1.1.3)以及式(1.1.4)可以推导电感两端电压VLV_L如下：

VL=−Ndϕdt=−dλdt=−dLiLdt=−LdiLdtV_L=-{N\frac {d\phi}{dt}}=-\frac{d\lambda}{dt}=-\frac{dLi_L}{dt}=-L\frac{di_L}{dt}

这里的负号由楞次定律导出，一般情况下省略不写，电感方程即为：

VL=LdILdt(1.3.1)V_L=L\frac{dI_L}{dt} \tag{1.3.1}

伏秒积(电压型方程)

由上面的公式：

VL=Ndϕdt=NdBAedt=NAedBdt=NAeΔBΔt(Ae指有效横截面积)V_L={N\frac {d\phi}{dt}}=N\frac{dBA_e}{dt}=NA_e\frac{dB}{dt}=NA_e\frac{\Delta B}{\Delta t} (A_e指有效横截面积)

得到电压型方程为：

VL=NAeΔBΔt或ΔB=VLΔtNAe(1.3.2)V_L=NA_e\frac{\Delta B}{\Delta t}或{\Delta B}=\frac{V_L{\Delta t}}{NA_e} \tag{1.3.2}

同时还可以导出来一个重要的概念——伏秒积：

Et=VLΔt=NAeΔB(1.3.3)E_t=V_L{\Delta t} =NA_e{\Delta B} \tag{1.3.3}

借助伏秒积(Et=VLΔtE_t=V_L{\Delta t})，可以帮助我们很好地分析各类带电感的开关拓扑在稳态时的输入输出电压关系。
由于电感是无源器件，因此在稳态的一个开关周期内，流入和流出电感的能量是相等的，即电感充能时的ΔB{\Delta B}和释放能量时的ΔB{\Delta B}在数值上相等，即在稳态时的开关断开和开关闭合时的电感上的伏秒积相等。
再借助KCL和KVL即可分析出稳态时的输入输出电压关系。这里略过不表。

电流型方程

由(1.3.2)的第一个式子和式(1.3.1)

VL=NAeΔBΔt=LΔILΔtV_L=NA_e\frac{\Delta B}{\Delta t}=L\frac{\Delta I_L}{\Delta t}

得到电流型方程为：

ΔB=LΔILNAe(1.3.4){\Delta B}=\frac{L{\Delta I_L}}{NA_e} \tag{1.3.4}

磁环电感

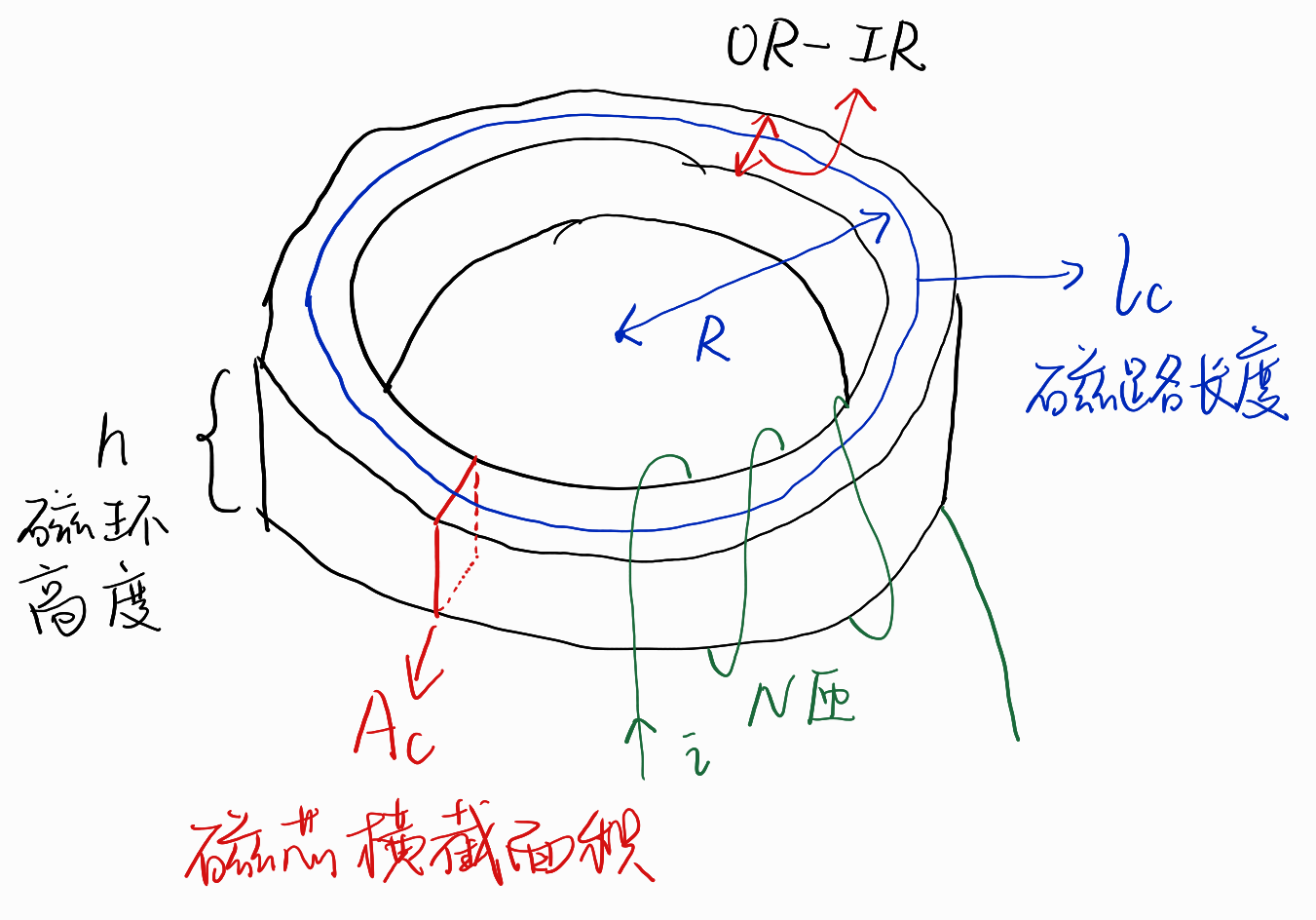
电感量推导

定义磁环的有效横截面积为AcA_c，内径为RR，有效磁路长度为lcl_c，磁导率为μc\mu_c(下标c指core)。当RR很大且内外径相近时，可以近似认为lcl_c就是内圈圆环的周长，即lc=2πRl_c=2\pi R。
现在缠上NN匝线圈，通入的电流的大小为ii。
由安培环路定律-式(1.2.1)得到：

H⋅lc=N⋅iH \cdot l_c=N \cdot i

即

H=NilcH= \frac{Ni}{l_c}

由式(1.1.1)、(1.1.2)和上式得到磁环内部磁通为：

ϕ=BcAc=μcHAc=μcNilcAc(2.1.1)\phi=B_cA_c=\mu_cHA_c=\mu_c\frac{Ni}{l_c}A_c \tag{2.1.1}

由式(1.1.3)得到磁链为：

λ=Nϕ=μcAcN2lci\lambda=N\phi=\frac{\mu_cA_cN^2}{l_c}i

由式(1.1.4)即可得知磁环电感为：

L=λi=μcAcN2lc=μcAclcN2(2.1.2)L=\frac{\lambda}{i}=\frac{\mu_cA_cN^2}{l_c}=\frac{\mu_cA_c}{l_c}N^2 \tag{2.1.2}

可以发现电感量正比于匝数的平方。

初步设计磁环电感

这里的初步设计是指如何选择合适尺寸的磁环以及绕多少匝的问题，电感量多大以及最大电感电流在选择完拓扑和确定好最恶劣工况后就已经确定下来，这里不展开赘述。

  1. 确定匝数
    式(2.1.1)得到了磁环电感的表达式L=μcAclcN2L=\frac{\mu_cA_c}{l_c}N^2，其中的μcAclc\frac{\mu_cA_c}{l_c}项称为电感系数ALA_L，电感厂商一般会直接给出(不给的买他家磁环干啥)。ALA_L的单位是nH/匝2nH/匝^2，即匝数的平方乘以ALA_L就是多少nH。

    N=L(nH)AL(2.2.1)N=\sqrt{\frac{L (nH)}{A_L}} \tag{2.2.1}

  2. 计算峰值磁通密度BmaxB_{max}
    这是很多人在设计电感时会忽略的一点，没有考虑到材料的物理极限，电感量不够就往上嗯加匝数，导致电流一大感量就哐哐往下掉甚至直接失效。
    由式(2.1.1)可知磁通密度为：

    B=μNilB=\frac{\mu Ni}{l}

    电流越大，匝数越多，磁通密度越大。但是一般的材料的磁通密度都会存在一个上限：饱和磁通密度BsatB_{sat}。一旦达到这个上限，磁通密度便不再增加，外在表现即为电感量下降，更严重的表现则是电感直接失效，失去所有感量。因此在设计电感时，必须时刻关注峰值磁通密度BmaxB_{max}。
    但是使用上面的公式来计算BmaxB_{max}似乎有些麻烦了，要手动计算有效磁路长度ll的大小。这里可以使用电感的电流型方程-式(1.3.4)来简化计算：

    Bmax=LImaxNAe(2.2.2){B_{max}}=\frac{L{I_{max}}}{NA_e} \tag{2.2.2}

    其中，LL和Imax{I_{max}}都是已知量，匝数NN也在上面计算得到，有效横截面积AeA_e厂家一般都会给出，没有给出自己通过内半径IRIR，外半径OROR以及磁环高度hh简单计算也能得到：

    Ae=h(OR−IR)A_e=h(OR-IR)

    Bmax的取值范围

    对于铁氧体来说，一般取0.2 ~ 0.3T。
    对于铁硅铝来说，一般取0.6 ~ 0.8T。
    对于铁镍来说，一般取1.0 ~ 1.2T。

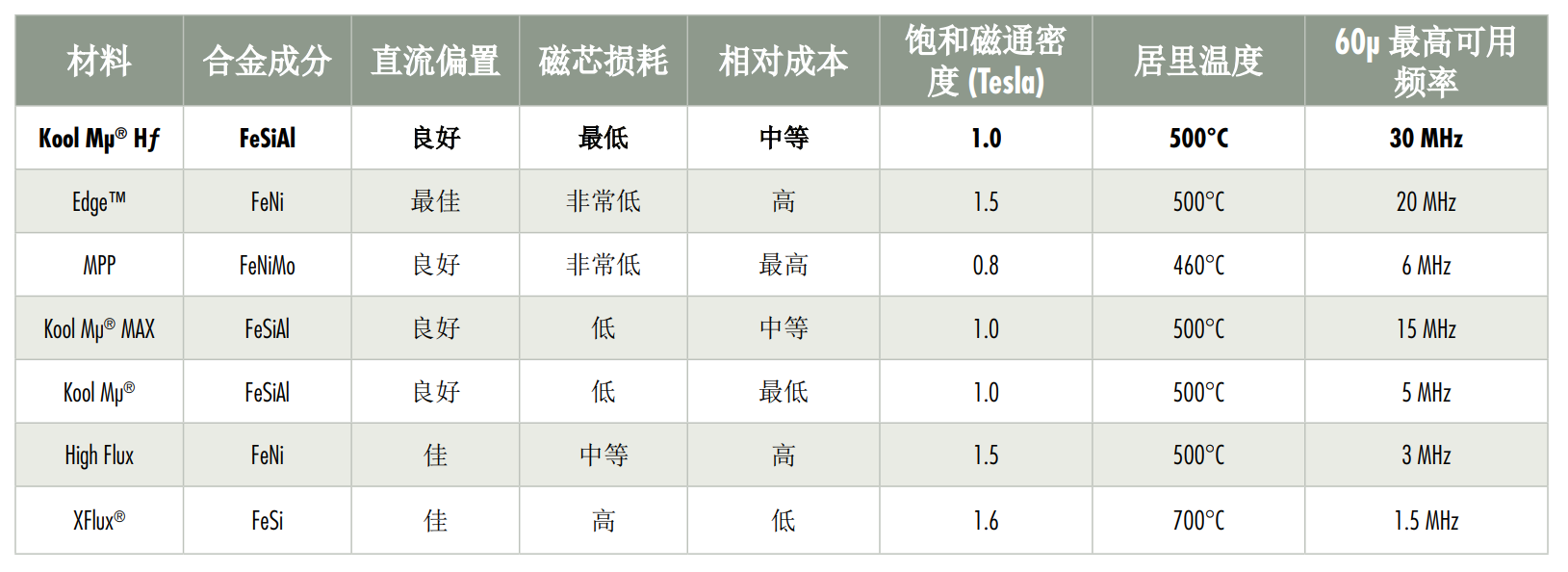
    美磁官方的表格，给出了铁硅铝(FeSiAl)和铁镍(FeNi)磁环的饱和磁通密度BsatB_{sat}

    假如说BmaxB_{max}肥肠极限，可以考虑如下的解决方法：

    1. 更换尺寸更大的磁环，更大尺寸的磁环的AeA_e更大，同时ALA_L也会变大，匝数NN会变小，但AeA_e的增加幅度更大，等效BmaxB_{max}是减小的。
    2. 相同尺寸的磁环叠绕。这样AeA_e直接翻倍，ALA_L也会翻倍，但是匝数NN变为12\frac{1}{\sqrt2}，等效BmaxB_{max}还是减小的。
    3. 使用磁导率μ\mu更小的磁环，这个减小了ALA_L，等效增加了匝数NN，也降低了BmaxB_{max}。
    4. 提高开关频率，降低ImaxI_{max}。
      但是注意，以上的方案都会增加绕线的长度，导致电感的铜损变大。
      可以把上面提到的东西扔到EXCEL表格中自动计算： 这里只是初步讲解了如何设计，设计好一个电感还有很多东西要考虑：磁通密度摆幅ΔB\Delta B，绕线的线径如何选择，绕线的窗口面积够不够，磁芯材料如何选择，磁损和铜损如何权衡，直流和交流的不同应用场景等等。

带有气隙的C字形磁环电感

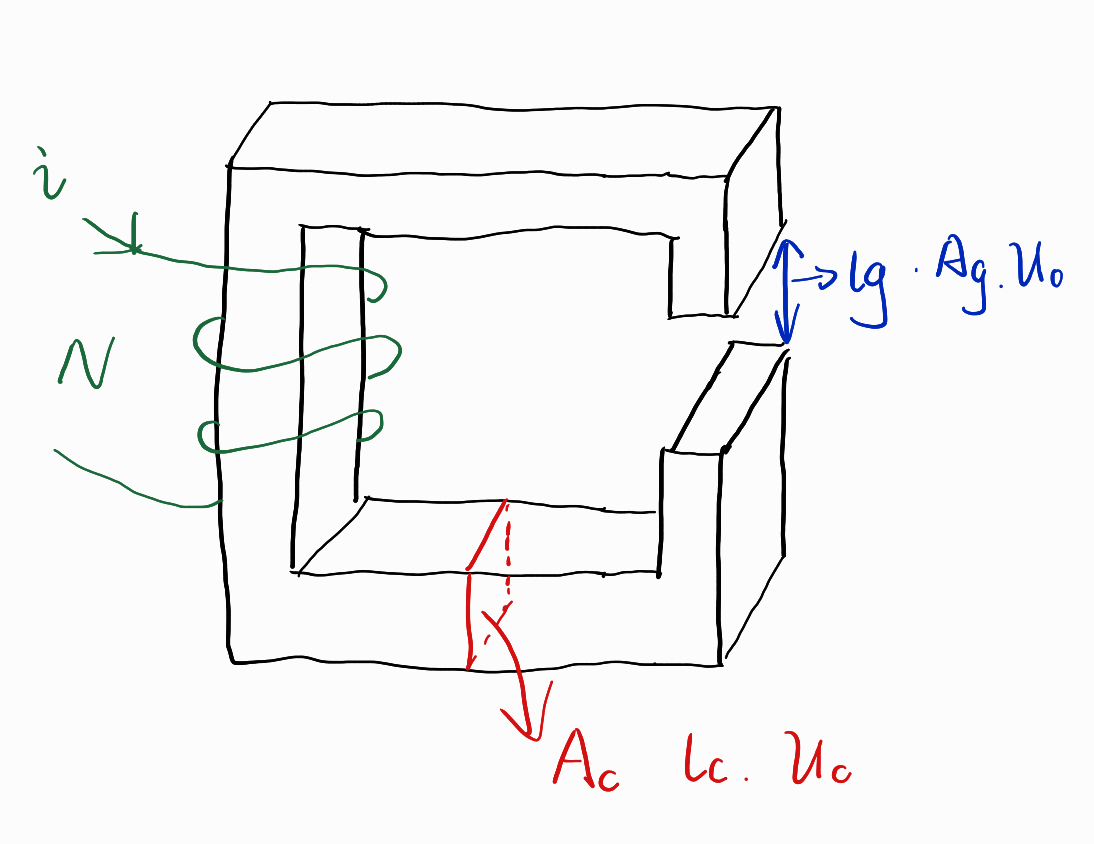依旧令磁芯内部的有效横截面积为AcA_c，有效磁路长度为lcl_c，磁导率为μc\mu_c。在气隙处的介质为空气，磁导率近似为真空磁导率μ0\mu_0，气隙长度为lgl_g,有效横截面积为AgA_g。
在磁芯和气隙的交界处，仍然认为磁场是均匀磁场，且垂直于磁芯表面，忽略磁芯边缘泄露出去的磁场。
因此可以认为：

Ac=AgA_c=A_g

由安培环路定律-式(1.2.1)得到：

Hclc+Hglg=Ni(3.1)H_cl_c+H_gl_g=Ni \tag{3.1}

磁芯内部和气隙处通过的磁通相等：

ϕc=BcAc=BgAg\phi_c=B_cA_c=B_gA_g

由式(1.1.2)-H=Bμ{{H} ={\frac {{B} }{\mu}}}得到：

ϕc=μcHcAc=μ0HgAg\phi_c=\mu_cH_cA_c=\mu_0H_gA_g

得到：

Hc=ϕcμcAc,Hg=ϕcμ0AgH_c=\frac{\phi_c}{\mu_cA_c},H_g=\frac{\phi_c}{\mu_0A_g}

将HcH_c和HgH_g代回式(3.1)得到：

ϕc(lcμcAc+lcμ0Ag)=Ni\phi_c(\frac{l_c}{\mu_cA_c}+\frac{l_c}{\mu_0A_g})=Ni

磁通ϕc\phi_c即为：

ϕc=NilcμcAc+lgμ0Ag=NiAclcμc+lgμ0\phi_c=\frac{Ni}{\frac{l_c}{\mu_cA_c}+\frac{l_g}{\mu_0A_g}}=\frac{NiA_c}{\frac{l_c}{\mu_c}+\frac{l_g}{\mu_0}}

磁链为：

λ=Nϕc=N2Aclcμc+lgμ0i\lambda=N\phi_c=\frac{N^2A_c}{\frac{l_c}{\mu_c}+\frac{l_g}{\mu_0}}i

电感即为：

L=N2Aclcμc+lgμ0L=\frac{N^2A_c}{\frac{l_c}{\mu_c}+\frac{l_g}{\mu_0}}

对于一般的磁性材料来说，μc\mu_c>>μ0\mu_0，因此lcμc\frac{l_c}{\mu_c}<<lgμ0\frac{l_g}{\mu_0}。这时候电感可以近似为：

L=N2Acμ0lgL=\frac{N^2A_c\mu_0}{l_g}

可以看出来，在磁芯上面开气隙之后，电感的感量和原磁芯的磁属性没有关系了，导磁率和磁路长度都和气隙相关了。
这个时候HgH_g>>HcH_c(因为μc\mu_c>>μ0\mu_0，H=Bμ{{H} ={\frac {{B} }{\mu}}})，Bg=BcB_g=B_c，根据下面计算磁场能量的式子：

Wm=12∫∫∫B⋅HdVW_{m}=\frac{1}{2}\int\int\int B\cdot H dV

可以得到，气隙中的能量远远大于磁芯中的能量。
气隙舍弃了一小部分磁芯，但是能储存远大于同等体积磁芯的能量，这似乎是一个解决2.2节最末尾提到的BmaxB_{max}很接近磁芯饱和磁通问题的一个好方法：在相同的磁通密度下，使用气隙来储存更多的能量，而不是使用更大的感量去存储能量。
事实上，在设计电感或者变压器时，开气隙是一个非常常见的手段，一方面使用气隙控制电感量，另一方面，使用气隙存储更多的能量。
但是这样做有一些坏处：由于气隙存储了大部分的能量，而且空气的导热能力远不如磁芯；同时为了降低漏感，气隙一般会被包在线圈里面，就会导致气隙会成为整个器件最热的地方。在批量生产时，电感量的精度比较依赖余气隙打磨的精度，所以一些小厂打磨的电感或者变压器的一致性就不会很好。

本文作者:zxcli

本文链接:

版权声明:本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！