第一篇笔记讲解了磁性器件中的电感,这一篇来讲一下变压器。
理想变压器
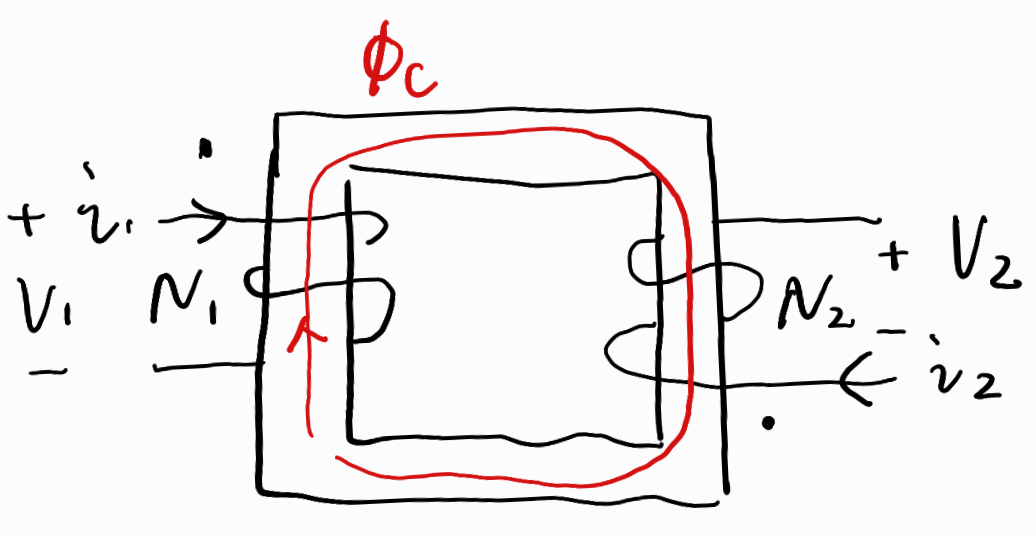 首先考虑绕在同一个磁芯上的两绕组理想变压器,左边绕组N1匝,通入v1,i1,右边绕组N2匝,通入v2,i2。定义如下物理量:磁芯有效横截面积为Ac、磁路长度为lc、磁导率为μc、磁芯中流动的磁通为ϕc。理想变压器满足这两个假设假设:μc→+∞;磁通ϕc无泄漏,全部被限制在磁芯中运行。
首先考虑绕在同一个磁芯上的两绕组理想变压器,左边绕组N1匝,通入v1,i1,右边绕组N2匝,通入v2,i2。定义如下物理量:磁芯有效横截面积为Ac、磁路长度为lc、磁导率为μc、磁芯中流动的磁通为ϕc。理想变压器满足这两个假设假设:μc→+∞;磁通ϕc无泄漏,全部被限制在磁芯中运行。
同名端
两个绕组的方向如图所示,当通入i1和i2时,磁芯两边产生的磁通在磁芯里面是绕着同一个方向运行的,我们就把这两个通入电流的端子称为同名端,用两个小黑点标识同名端。当电流从同名端通入时,磁通沿同一个方向流动,是相互增强的。
等效磁路
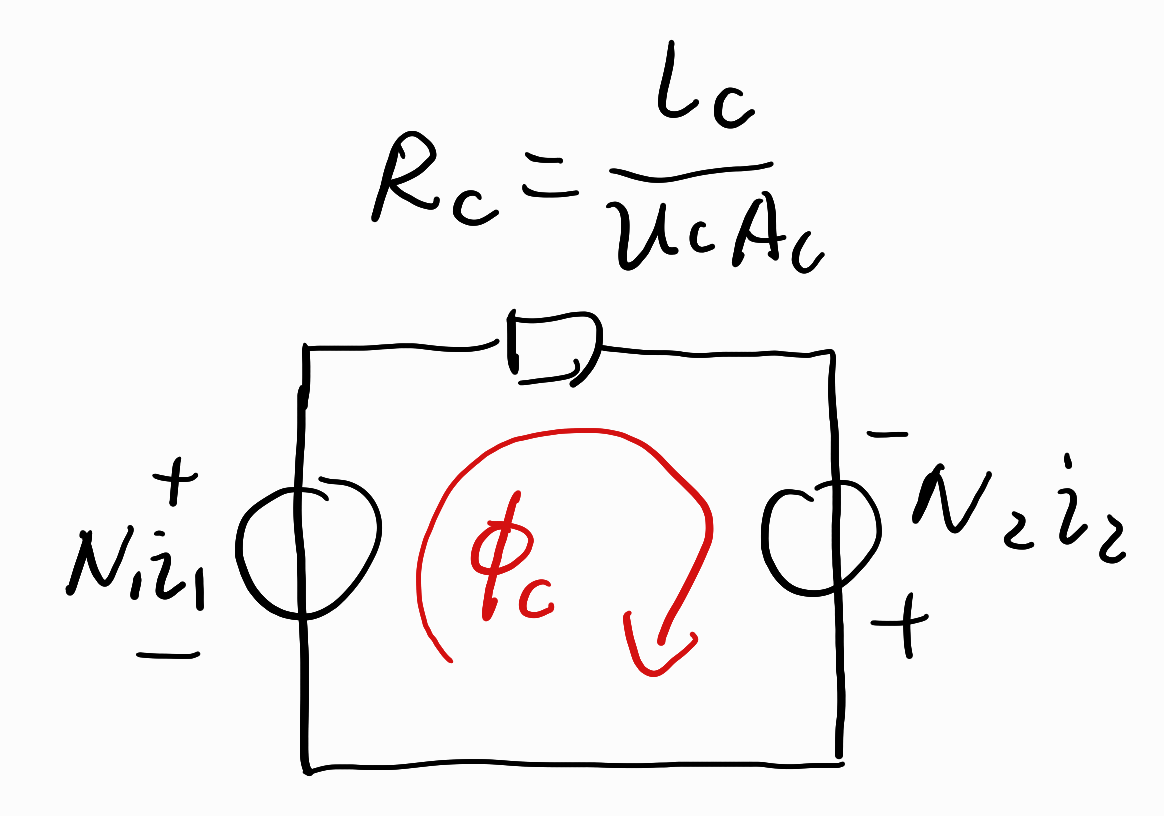 上面是理想变压器的等效磁路模型。
上面是理想变压器的等效磁路模型。
电压关系
左边绕组的磁链为:
λ1=N1ϕc
右边绕组的磁链为:
λ2=N2ϕc
根据法拉第电磁感应定律:
v1=dtdλ1=N1dtdϕc,v2=dtdλ2=N2dtdϕc
两式一比就得到:
v2v1=N2N1
电流关系
对于上面的磁路,可以列出方程:
N1i1+N2i2=ϕcRc
理想变压器假设了μc→+∞,磁阻Rc=μcAclc→0。
上面方程的右边就等于0:
N1i1+N2i2=0
就得到电流关系:
−i2i1=N1N2
这里的−i2意味着在右边的绕组上,电流i2实际的方向是由同名端流出(i1从同名端流入时)。可以看出来,两边绕组产生的磁动势是完全相同而且正负方向也是一样的,也就意味着理想变压器中没有净磁通流动,说明理想变压器是不存储能量的,仅起到电压变换和电流变换的作用。
实际电压电流方向:
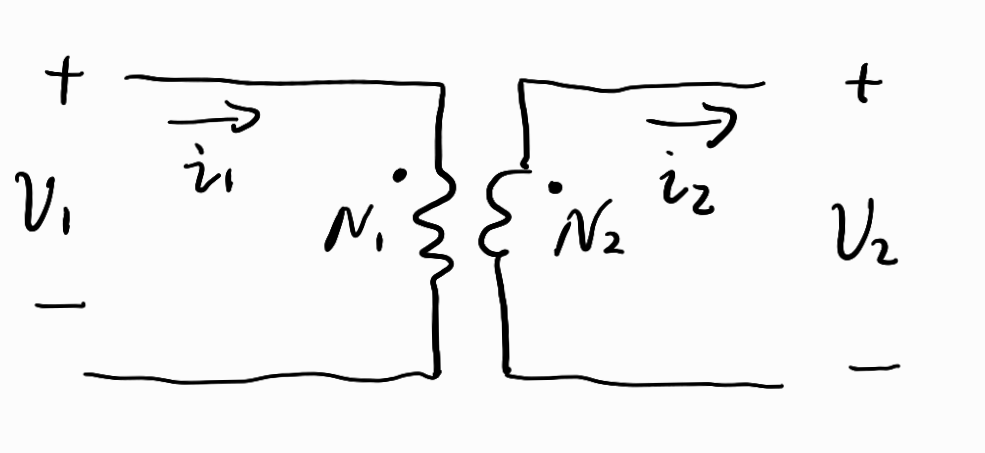 对于理想变压器,同一时刻,同名端处的电压极性相同(楞次定律分析即可),电流从一个同名端流入,从另一个同名端流出。两端电压电流满足:
对于理想变压器,同一时刻,同名端处的电压极性相同(楞次定律分析即可),电流从一个同名端流入,从另一个同名端流出。两端电压电流满足:
v2v1=N2N1,i2i1=N1N2
非理想变压器
上面对于理想变压器的分析引入了两个假设:μc→+∞;磁通ϕc无泄漏。当设计真正的变压器时,这两个假设自然是不成立的,下面分析一下考虑μc有限和存在漏磁的情况。
μc有限
当μc有限时,也就意味着ϕc不为0。这个时候将右边的绕组闲置不接任何东西,左边的绕组加上磁芯就能看成一个电感Lμ1:
Lμ1=RcN12
这时候的变压器模型就是这样:
 本来不存储任何能量的理想变压器,现在多出来一个电感Lμ1,还在Lμ1上多出来一个电流iμ1来额外推拉输入该绕组的电流。iμ1只起到磁化磁芯,使其内部产生磁场的作用,因此把这个电流称为励磁电流,Lμ1称为励磁电感,其中储存的能量为21Lμ1iμ12。
本来不存储任何能量的理想变压器,现在多出来一个电感Lμ1,还在Lμ1上多出来一个电流iμ1来额外推拉输入该绕组的电流。iμ1只起到磁化磁芯,使其内部产生磁场的作用,因此把这个电流称为励磁电流,Lμ1称为励磁电感,其中储存的能量为21Lμ1iμ12。
考虑此时Bmax的大小
- 当N1通入电流iμ1时,Lμ1磁化,在磁芯中产生主磁通ϕμ1。
- N2在主磁通ϕμ1的感应下,产生感应电动势v2。同时因为N2不再闲置,产生电流i2。
- 根据楞次定律,电流i2会阻碍磁通的变化。因此,电流i2会产生一个磁动势N2i2,N2i2会产生一个和主磁通方向相反的磁通,去试图削弱主磁通ϕμ1。这个磁通称为去磁磁通。
- 假如主磁通真的被削弱了,会导致N1绕组上的感应电动势减小。但感应电动势和v1等值方向相反,而v1是定值。因此主磁通ϕμ1不能被削弱。
- 主磁通ϕμ1不能被削弱,N1绕组则会尝试吸取额外的电流i1,形成新的磁动势N1i1。这个磁动势去尝试增加磁通,抵抗去磁磁通的削弱。最后的结果则是N1i1和N2i2正好抵消。
- N1i1和N2i2抵消掉之后,主磁通仍然是ϕμ1。
可见,最后磁芯内部的磁通取决于励磁电感Lμ1上产生的磁通,在考虑Bmax限制时只需约束它产生的磁通密度即可。
Lμ1成为了变压器的限制,那是不是励磁电感就毫无用处了呢。并非如此:反激变换器使用励磁电感存储能量;LLC变压器使用励磁电流在死区内抽取MOS的Coss上的电荷,来实现ZVS。
存在漏磁
在上面的分析中,N1和N2都会产生磁通,理想状态下所有的磁通都会与线圈相交链,但是实际上会有些许磁通泄露出去:
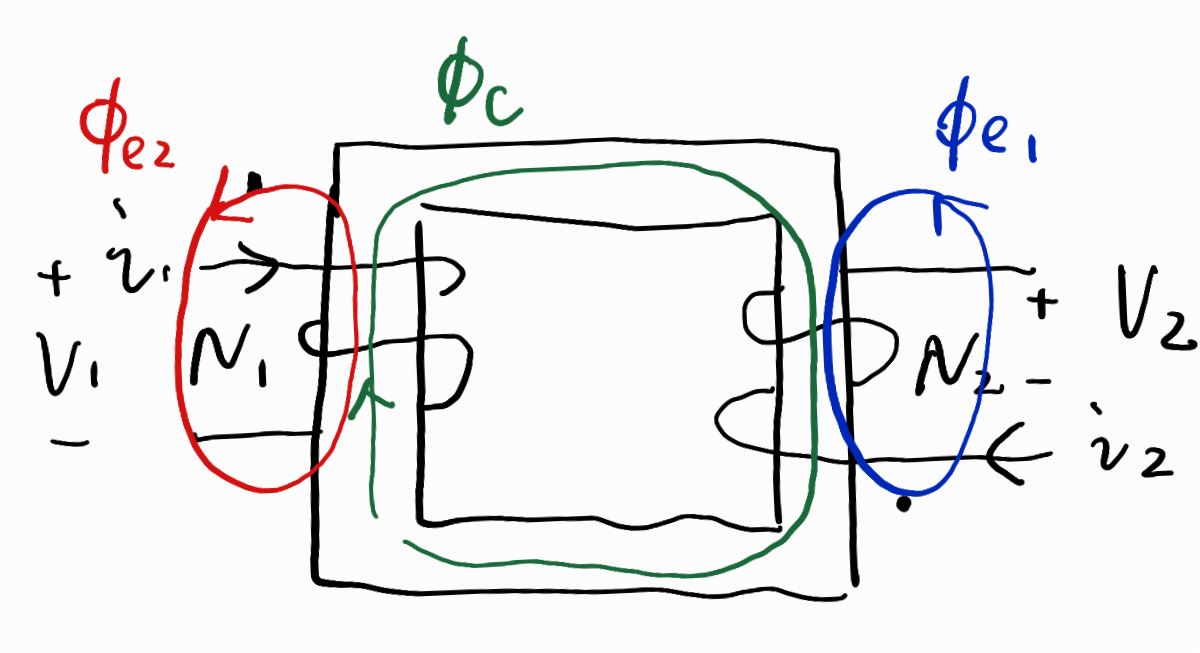 等效磁路如下:
等效磁路如下:
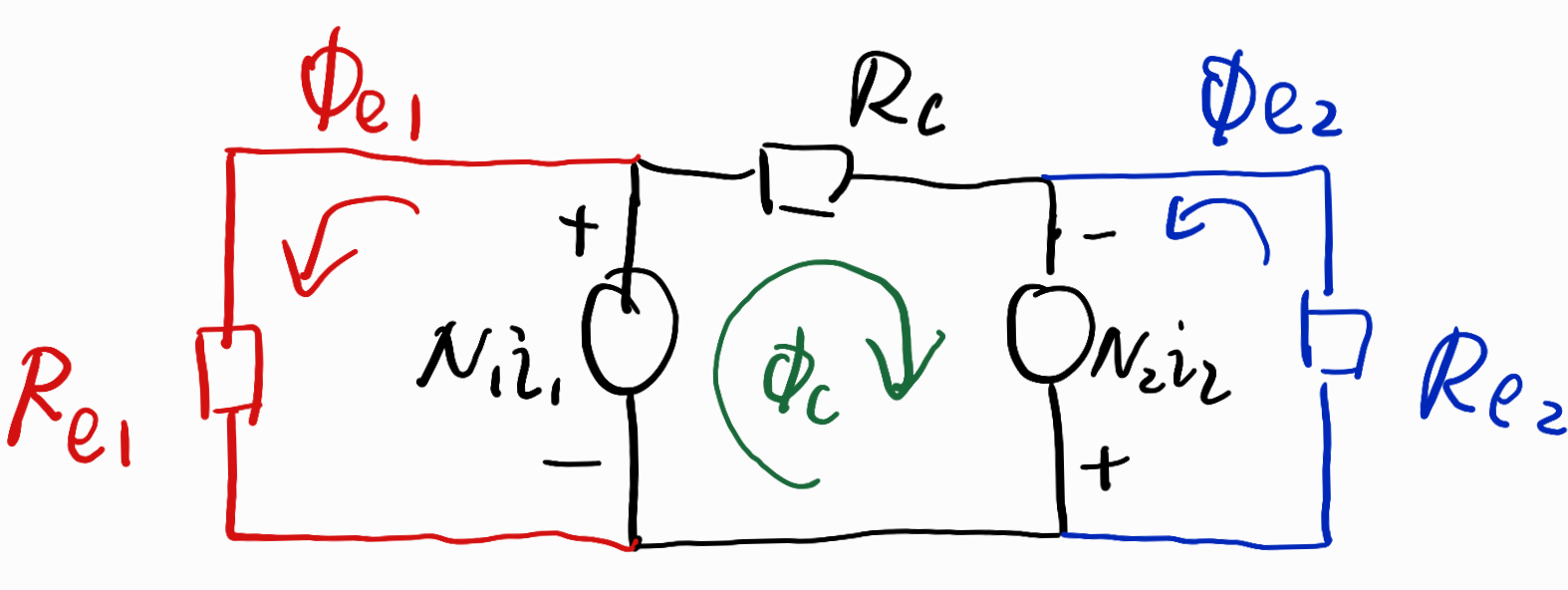 漏磁通ϕe1:
漏磁通ϕe1:
ϕe1=Re1N1i1
漏磁通ϕe2:
ϕe2=Re2N2i2
主磁通ϕc:
ϕc=RcN1i1+N2i2
N1和N2上的磁链λ1、λ2分别为:
λ1=N1(ϕe1+ϕc)=Re1N12i1+RcN12i1+RcN1N2i2
λ2=N2(ϕe2+ϕc)=Re2N22i2+RcN22i2+RcN1N2i1
写成矩阵形式:
[∫v1dt∫v2dt]=[λ1λ2]=[Re1N12+RcN12RcN1N2RcN1N2Re2N22+RcN22][i1i2]⇒[v1v2]=[L11LMLML22]dtd[i1i2]
等效电路模型可以画成这样:
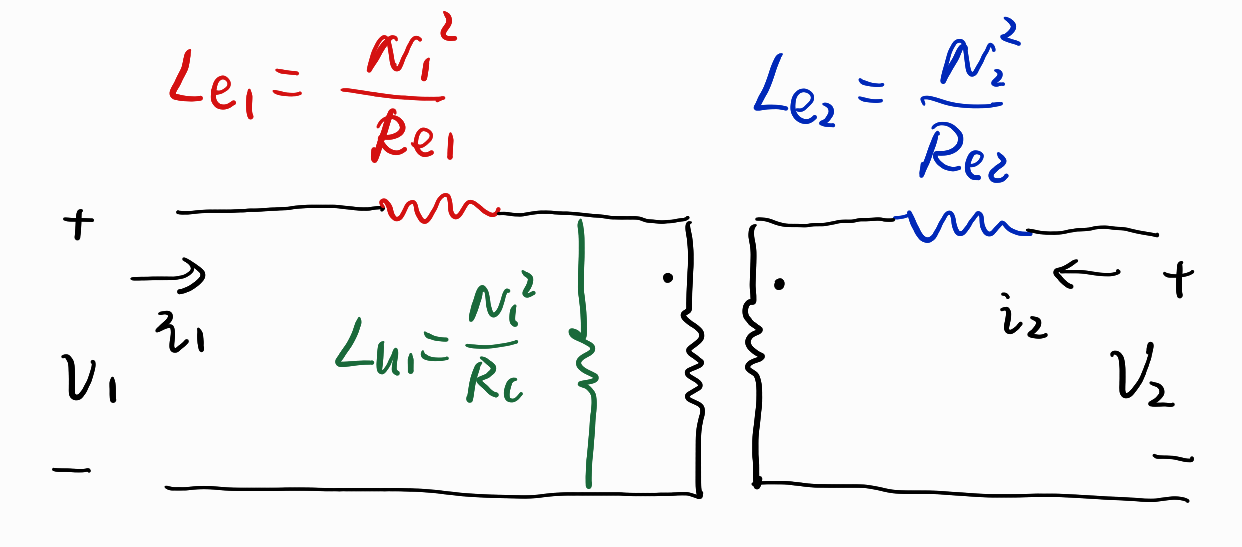 Lμ1是初级励磁电感,Le1是初级漏感,Le2是次级漏感。
Lμ1是初级励磁电感,Le1是初级漏感,Le2是次级漏感。
这个模型称为T-模型,有:
L11描述的是变压器初级的总自感
L11=Le1+Lμ1
L22描述的是变压器次级的总自感
L22=Le2+(N1N2)2Lμ1
LM描述的是变压器两个绕组的互感
LM=N1N2Lμ1
初次级的电压:
v1=L11dtdi1+LMdtdi2
v2=LMdtdi1+L22dtdi2
初级电压由两部分组成:自身电流变化产生的自感电压 + 次级电流变化通过互感耦合过来的电压。
次级电压同样由两部分组成:互感耦合的电压 + 自身电流变化产生的自感电压。
 首先考虑绕在同一个磁芯上的两绕组理想变压器,左边绕组匝,通入,右边绕组匝,通入。定义如下物理量:磁芯有效横截面积为、磁路长度为、磁导率为、磁芯中流动的磁通为。理想变压器满足这两个假设假设:;磁通无泄漏,全部被限制在磁芯中运行。
首先考虑绕在同一个磁芯上的两绕组理想变压器,左边绕组匝,通入,右边绕组匝,通入。定义如下物理量:磁芯有效横截面积为、磁路长度为、磁导率为、磁芯中流动的磁通为。理想变压器满足这两个假设假设:;磁通无泄漏,全部被限制在磁芯中运行。 上面是理想变压器的等效磁路模型。
上面是理想变压器的等效磁路模型。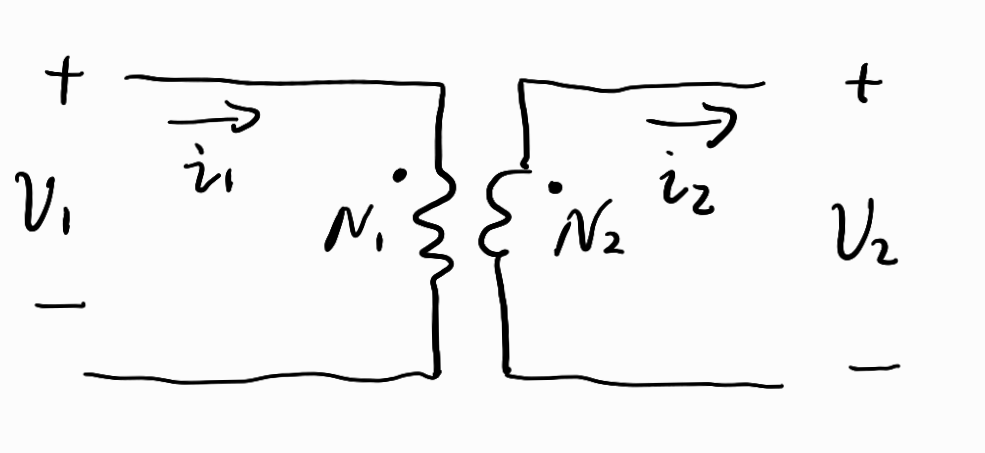 对于理想变压器,同一时刻,同名端处的电压极性相同(楞次定律分析即可),电流从一个同名端流入,从另一个同名端流出。两端电压电流满足:
对于理想变压器,同一时刻,同名端处的电压极性相同(楞次定律分析即可),电流从一个同名端流入,从另一个同名端流出。两端电压电流满足: 本来不存储任何能量的理想变压器,现在多出来一个电感,还在上多出来一个电流来额外推拉输入该绕组的电流。只起到磁化磁芯,使其内部产生磁场的作用,因此把这个电流称为励磁电流,称为励磁电感,其中储存的能量为。
本来不存储任何能量的理想变压器,现在多出来一个电感,还在上多出来一个电流来额外推拉输入该绕组的电流。只起到磁化磁芯,使其内部产生磁场的作用,因此把这个电流称为励磁电流,称为励磁电感,其中储存的能量为。 等效磁路如下:
等效磁路如下:
 漏磁通:
漏磁通: 是初级励磁电感,是初级漏感,是次级漏感。
是初级励磁电感,是初级漏感,是次级漏感。